【聖經】財務自由，靠“投機”能實現嗎？

一、首先，我們要區分一下：投資、投機、賭博之間，到底有什麼區別？

看起來，這三者都充滿了不確定性。企業家和投資家們，也經常喜歡說：讓我們賭一把吧。

說起來，好像都是為看不見的未來下注：賭贏了就是投資成功；贏得驚險賺得很多就是投機成功；失敗了便被視為“賭輸了”。人生一場，誰不是賭呢？這種想法，其實是不思進取、不動腦子的自暴自棄。

為了避免掉入毫無意義的講大道理和文字遊戲，在這裏，我想用一個簡單粗暴的方式來定義：

期望值為正的，是投資；

期望值是負的，是賭博；

期望值未知的，是投機。

有投資經驗的客官可能會說了，你這不是廢話嗎？既然說了是不確定性，就很難分清期望值是正是負。要是知道期望值，誰不會賺錢啊？果真如此嗎？未必。

本文的前幾部分看起來很簡單。不過，現實中，我們犯的絕大多數錯誤，都出現在簡單的常識方面。

我將事件的不確定性、時間的不確定性和籌碼的不確定性整合在一起，去探尋如何用概率思維來構建一個體系。何妨一起重溫一下？

二、期望值的概念雖然非常簡單，但真正能搞明白的，沒多少人，在人群中也許小於1%。

曾翻過一本據說賣了幾十萬冊的暢銷書，裏面有一節講概率，作者居然混淆了概率、賠率、期望值等基本概念。讓我們從頭復習一下期望值：

在概率論和統計學中，一個離散性隨機變數的期望值（或數學期望，亦簡稱期望，物理學中稱為期待值）是試驗中每次可能的結果乘以其結果概率的總和。換句話說，期望值像是隨機試驗在同樣的機會下重複多次，所有那些可能狀態平均的結果，便基本上等同“期望值”所期望的數。舉個例子，你一直扔一個骰子很多很多次，你得到每一個的可能性是一樣的，那麼你扔一個骰子的期望值就是：

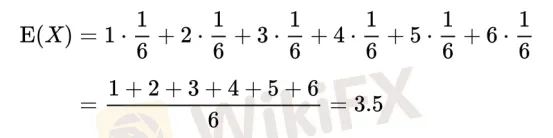
那麼，由此可以計算得出，擲一枚公平的六面骰子，其每次“點數”的期望值是3.5。這是無限多次重複後，得到的一個平均值。

三這麼簡單的一個框架，是幾乎所有投資高手必備的第一公式。魯賓舉過一個高盛的投資套利的案例。

有一次，在某兩家公司宣佈合併之後，高盛打算做一次套利。儘管宣佈了消息，但是該合併可能成功，也可能失敗。

高盛打算買入其中的W公司，當時股價是30.5美元。如果合併事宜談妥的話，W公司的股價上漲可能3美元；如果合併失敗，W公司的股價有可能下跌6美元左右。

這相當於是對骰子上面的數字估值，接下來還要估一下每一面出現的可能性。

把合併成功的可能性定為大約85%，失敗的可能性為15%。接下來，我們計算一下期望值：股價可能上漲的幅度是3美元乘以85%，而下跌的風險是6美元乘以15%。

3美元×85%=（可能上漲）2.55美元

-6美元×15%=（可能下跌）-0.9美元

二者相加，該投資的期望值是每股1.65美元 。

該投資計畫三個月內完成：

每股期望值是1．65美元

本金是30.50美元

3個月的可能回報率為5.5%，

年化回報率可能為22%。

普通人看這個案例，可能會覺得滿頭霧水：漲多少跌多少錢是猜的，漲跌的可能性也是猜的，這種計算有意義嗎？

期望值的計算，提供了一個分析框架，用於面向不確定性未來的決策和下注。

對於股價可能的漲幅和跌幅，有賴於專業能力與經驗。

對於交易是否可能完成，有賴於專業以及情報。

以上兩件事情水準再高，也需要放在期望值計算的分析框架下，才能與不確定性共舞。不管這次交易預測得多麼准，結果都可能是出乎意料的，與期望值相去甚遠。

就像扔骰子，期望值是3.5，但是你扔出一個6的可能性還是有1/6。但是，假如你扔很多次，你就會很接近期望值。所以，期望值的計算，提供的是一種“模糊的精確”，重複次數越多，就越精確。

四儘管計算這麼簡單，期望值讓很多專業人士都犯暈。塔勒布就曾經嘲笑索羅斯曾經的搭檔羅傑斯，說對他這樣一個連期望值都弄不明白的傢伙，賺的錢有點兒太多了。

似乎華爾街也有很多人不懂。塔勒布在一次投資研討會說：“我相信下個星期市場略微上漲的概率很高，上漲概率大概70%。”但他卻大量賣空標準普爾500指數期貨，賭市場會下跌。當時很多人不明白啥意思。他的意見是：市場上漲的可能性比較高（我看好後市），但最好是賣空（我看壞結果），因為萬一市場下跌，它可能跌幅很大。假使下個星期市場有70%的概率上漲，30%的概率下跌。但是如果上漲只會漲1%，下跌則可能跌10%。未來預期結果是：70%×1%+30%×（-10%）=-2.3%，因此應該賭跌，賣空股票盈利的機會更大。讓我們在回到本文開頭的觀點：

期望值為正的，是投資；

期望值是負的，是賭博；

期望值未知的，是投機。

高盛的案例，看起來是期望值為正的投資。塔勒布的下注，看起來像期望值未知（只是“我相信”）的投機。那麼賭博呢？以美國的輪盤賭為例：

常用的輪盤上有38個數字，每一個數字被選中的概率都是相等的，也就是1/38。

你下注在某一個數字上，如果押中，賺相當於賭注35倍的獎金（賭注不包含在內），若沒押中，你輸掉賭注。

我們來算一下期望值，假如你每次押1塊錢：

贏的概率是38分之1，能獲得35元；

輸的概率是38分之37，虧掉1塊錢。

35×1/38-1×37/38，結果約等於-0.0526元。

也許你偶然會押中，本錢變成36倍，甚至押中了好幾次，但是只要你持續玩兒下去，大數定律就會發揮作用，你會穩穩地輸光所有本錢。所以，這個世界上靠“穩定”的概率來賺錢的，也許只有賭場老闆。反過來，假如你是一個想追求穩定概率的賭徒，你會輸得很穩定，窮得很穩定。

何止是賭徒，在現實中，為了虛幻的確定性，人們願意做任何事情。

五好了，假設我們都知道了“期望值”這個概念，也暫時假設我們對於漲幅跌幅以及對應的發生概率估算很靠譜，那麼是不是就可以走在成為投資高手的路上了？還是不行。2016年，物理學家奧利.彼得斯和諾貝爾物理學獎得主默裏.蓋爾曼寫了一篇關於遍曆性的論文，裏面有個例子：有個玩硬幣的賭博遊戲，你投入1元，50%可以得到0.6元，50%可以得到1.5元。根據期望值計算，一半可能性損失40%，一半可能性盈利50%，算下來數學期望是5%。用流行的話說，這是大概率賺錢的事情，你可以大膽玩這個遊戲。不過，這個遊戲有兩種玩兒法，確切說，是有兩種不同的下注方式：

方式a：你每次都拿1塊錢去玩，假設你有無限多個1塊錢，你可以一直玩下去，從長期來看你肯定是賺錢的，平均每把用5%的數學期望算是0.05元。缺點是太慢，而且你必須有足夠多的時間能玩下去。方式b：拿出自己能拿出的最大的資金，然後投入進去。後面這種玩兒法，就是所謂的All in。看起來極端，其實很多人都是這麼幹的，我自己也經歷過，誰沒年輕（蠢）過啊。

我們來做個簡單的計算吧。

你本金一百萬，第一把贏，第二把輸，第三把再贏，如此持續下去。

直覺上看，100萬本金，贏了是賺50萬，輸了是虧40萬，為什麼不能玩兒呢？

拿張紙，用中國當前幼稚園小班的數學能力計算一下：

100萬✖️（1+50%）✖️（1-40%）✖️（1+50%）（1-40%）......一直這麼玩兒下去，你會發現，沒有幾把就沒錢了。

這難道不是絕大多數普通人做投資的現實嗎？韭菜自己被割起來更加無痛，沒準兒還覺得是自己被割的時候姿勢沒擺好，天天繼續勤學苦練，把辛辛苦苦的錢接著拿去All in下一個風口。這裏計算的關鍵，是算術平均值和幾何平均值之間的差別。假如你花100萬買了一只基金，第一年漲了100%，第二年跌了50%。那麼你的收益是多少？按照算術平均值計算：平均收益率=(第一年收益率+第二年收益率)/2=(100%-50%)/2 = 25%。按照幾何平均值計算：年收益率假設是x，（1+x）×（1+x）=（1+100%)×(1-50%)=1，計算結果，x=0。也就是說，按照幾何平均數算，年回報率是零。實際就是如此。這裏用幾何平均值計算出來的回報率，就是所謂“年化回報率”。對比而言：“年化回報率”（幾何平均收益率）更準確地反應基金實際的歷史收益情況；算術平均收益率放大了投資的收益率。下次買基金，記得問一下：這只基金多久了？這個回報率是算術平均值還是幾何平均值？

六至此，又出現了一個與“不確定性”相關的要素，那就是：籌碼。期望值為事件和時間的不確定性提供了一個框架，但不包括籌碼。即使你對不確定性事件有足夠的洞見，假如你不能把握好下注的數量，時間就不能成為你戰勝不確定性的朋友。

你下注比例太小，可能賺得太慢；

你下注比例太大，可能會虧光本金；

即使獲勝概率更大，期望值也為正，如果你次次all in，也可能因為幾何平均值而被割光了韭菜。

這時，一條投資真理冒了出來：在成功之前，你必須活下來。金融傳奇人物索普，在試圖戰勝賭場的過程中發現，即使你洞察了賭場的漏洞，找到了期望值為正的機會，也要面臨“如何決定賭注大小”的挑戰。

另一位天才香農建議他參考約翰·凱利1956年發表的文章。香農把它稍做修改後將其作為21點、輪盤賭、其他賭博、體育博彩和股市的下注原則。凱利公式遵循的是幾何平均值最大化的準則，使用該公式決定每次下注金額占本金的比例，能夠讓投資者每一個時期都最大化組合收益的幾何平均值。經濟學家們對幾何平均值和凱利公式有著長久的爭執，但是對於普通人而言，只用記住一點：不管凱利公式多厲害，只對“期望值為正”的下注有效。簡單說，這個公式只幫助想做有價值投資的人，對於賭博（期望值為負），毫無意義。

這就是為什麼我用期望值來作為區分投資、投機與賭博。

七讓我們再看回下凱利公式。該公式沒有強調的是：

你的本金是固定的嗎？換句話說，你用於下注的本金，會像泉水一樣越來越多嗎？職業投資人和業餘投資者最大的區別之一，在於職業選手有源源不斷的彈藥。

巴菲特有保險公司的浮存金，可以發債（不差錢的他今年四月在日本借了18億美金）。

他還強調所投公司有很好的自由現金流，他有一個極小的總部，只在乎旗下公司的經理人們把賺到的錢源源不斷地交上來。據知情人士稱，高瓴2020年上半年正在從投資人那裏籌措可能多達130億美元的資金，準備抓住疫情之下經濟當中出現的新機會。上一次融資是在2018年，最終募集到106億美元，創造了紀錄。據得州大學捐贈基金的數據顯示，扣除費用之後，高瓴截至2019年6月的近十年年平均回報率大約是20%。也許有人會意外，這麼牛的公司，年回報也“才”20%呀！

當然，事實是連續十年年回報20%，已經很驚人了。

重點在於，即使牛如巴菲特和高瓴，也在源源不斷地獲得資金，為下一次下注準備籌碼。只有如此，無限遊戲才可以持續下去，英雄一直留在場上，大數定律發揮作用，財富因為遍曆性中的概率優勢、以及最大化的正期望值得以實現。這才是“長期主義”背後的道理。

八投資很難，為未來下注，從不確定性中賺錢，對誰都是很難的事情。

沒誰是靠水晶球賺錢的。

2018年蔚來上市時，高瓴在蔚來的持股比例高至7.5%。2019，張磊繼續下注於新能源汽車賽道，增持蔚來至12%，還新買入66.83萬股特斯拉的股票。結果，因為新能源汽車補貼滑坡，以及燃油車因國六標準出臺甩賣，蔚來的股價最低跌至1美元。

張磊接下來清盤了蔚來和特斯拉，就在特斯拉大漲的前夜。時至今日，蔚來的股價已經漲回到近28美元。舉蔚來和特斯拉的例子，不是說張磊不厲害，也不是想像某些文章去談“張磊的長期主義你們學不會”，而是想說：

1、沒人能夠預測短期的未來，在某個時間“看錯”某筆投資，太正常了；

2、一個成熟的投資者不需要維持自己的“無比正確”，只需要從概率和期望值層面獲勝就好了；

3、作為一只越來越大的基金，在某些領域的投資見好就收，避免回撤，也能實現較好的幾何平均回報；

4、高瓴2020年7月回頭又重金了小鵬汽車。

九也許你還記得開篇時我埋下的一個火種：你憑什麼估算出一筆投資的期望值？

你怎麼知道買了一只股票，可能漲10塊錢，發生的可能性是60%；可能跌5塊錢，發生的可能性是40%。這麼多可能性，疊加在一起，不就更加不可能了嗎？期望值計算，提供了一個應對不確定的框架；

凱利公式，提供了一個根據本金比例下注的準則；獲取資金，為投資人提供了源源不斷的彈藥。然而，想要取得像高瓴那樣年20%的回報，你還需要做到更多。概括而言：

一個是獲取更好的投資標的：

一個是介入公司讓價值上漲的概率變大，從而主動提升專案回報的期望值。

前者，我稱之為資源；

或者，則為賦能。張磊將自己在人大和耶魯的校友圈用的淋漓盡致，他會在香港的豪華遊艇上接待投資圈與企業界的牛人們，人脈在東方國度對投資而言有著更重的分量。

至於賦能，這方面的案例就多了，通過合作、技術等。

因為資源，能拿到更好的專案；

因為賦能，能夠讓專案的回報期望值更高。

在完成了以上種種，再加上時機和運氣，高瓴才為客戶實現了20%的年回報。

十我們一直沒有意識到，自己非常幸運地出生在一個充滿了奇跡的時代。中國過去30年的快速而長時間的增長，在人類歷史上都極其罕見。但因為我們身處其中，就覺得習以為常，好比坐慣了高鐵的人，對風馳電掣司空見慣。另一方面，民間文化對於頭部牛人的推崇，其實強化了彩票頭獎效應，也讓很多人認為賭場必有秘笈。人們習慣了賭，崇拜賭場贏家。

人們為錯過房地產焦慮，為錯過騰訊焦慮，為錯過比特幣焦慮。

遍地都是十倍、百倍回報的傳說，讓人晚上睡不好覺。

這種對於頭部贏家的拜神，對普通人最大的傷害，就是讓人陷入了“小數陷阱”，誤把一些極小概率的事情當作常態。然而現實是，即使是在高速增長的時代，投資也是一件非常難的事情。很少有人因為回報低而貧困，但太多富人因為追求更高的回報而虧光辛辛苦苦賺來的錢。那些錢大多來自大時代的超級運氣，幾乎都無法再次重現。

最後總結一下：

1、遠離賭博，謹慎投資，儘量別投機，去做正期望值的事情；

2、投資有虧有賺，別試圖靠預測賺錢，要靠概率和正期望值；

3、投資很難，我們要放低獲得超額回報的預期，追求合理回報；

4、下注需要控制比例，拉長時間；

5、要有源源不斷的現金流。小心那些不產生現金流的固定資產投入，哪怕有些看起來可能有很大“漲幅”；

6、發財之前別掛掉；

7、對於年投資回報率，幾何平均值比算術平均值更重要；

8、別去參加那些零和遊戲；

9、努力創造價值，做創造價值的工作，投資於創造價值的公司；

10、關於財務自由，請記住：金錢如海水，越喝越渴。一旦你把財務和自由放在一起，其實是為自由戴上了枷鎖。