賭博、投資與逃命的學問：華爾街一線操盤手乾貨分享!

賭 博和投資取得成功的先決條件都是要做好防守，保住本錢，然後耐心等待真正的機會。總而言之，絕對不能在勝利前犧牲。

本文根據漁陽博客整理而成，作者客居美國，精通算術、賭 博和投資，好讀書，愛琢磨，著有《亂世華爾街》一書。

賭 博與投資系列之一：活著最重要

近來發現，不少讀者對《亂世華爾街》最感興趣的部分是開篇關於賭 博的那一段。看來21點畢竟比利率掉期更貼近群眾。其實賭 博和投資頗多相似，賭場裡的經歷也對我在華爾街當交易員極有説明。書裡由於篇幅所限，未能詳細討論，準備在博客裡展開談談。

講到賭 博和投資，人們通常都急於學會賺錢的招數，其實我個人認為賺錢方法是不容易學的，需要很多經驗和悟性。初學者要迅速提高“段位”，倒是應該重點先練練防守。防守是有一定套路，可以學習的。

在我看來，賭 博和投資取得成功的先決條件都是要做好防守，保住本錢，然後耐心等待真正的機會。總而言之，絕對不能在革命勝利前犧牲。別以為這很容易做到，且不說我們周圍那些“發財未遂身先死”的賭友股友，即便在投資界絕頂高手中，從雲端跌落者也大有人在。且看幾個例子:

傑西-利弗莫爾：《股票作手回憶錄》中的主人公，投機界不世出的天才，從白手起家一直做到1929年時的一億美元身價，最終申請破產，並於數年後自 殺。

約翰-麥瑞威瑟：曾是王牌投行索羅門兄弟公司的超級交易員，後來創建了群星薈萃的長期資本對沖基金（LTCM），一度擁有40億美元的龐大資本，卻在1998年俄國債券危機中幾乎損失殆盡。（《亂世華爾街》中有關於LTCM危機的詳細分析。）

管金生：1988年創辦萬國證券，曾被譽為“中國證券之父”，卻在1995年“3.27國債事件”中馬失前蹄，以致身陷囹圄。

唐萬新：曾經統帥德隆系企業集團，傲視中國資本市場，終因資金鏈斷裂導致德隆帝國土崩瓦解。

上述諸人都可稱是資本市場的奇才，最終卻都失敗了。他們的經歷告訴我們：不注意控制風險，就會發生《漁夫和金魚》中的那一幕：努力奮鬥當上了教皇，結果又變回了海邊的小木屋。

賭 博與投資系列之二：沒有把握，絕不出手

很多年前，我經常從紐約的中國城坐“發財大巴”去大西洋賭城，同車的多是在餐館髮廊裡打工的勞動人民。他們大都企望在賭場裡改變命運，結果卻往往是送掉了微薄的薪水。記得有一次，鄰座的女孩說她每個星期都去賭場玩百家樂，還有一套取勝秘訣云云。回程的時候聊天，我贏了800美元，她輸了4000。我頓時興致大減，4000美元應該是她一個多月的收入！

看著滿車衣著簡樸的同胞，我忽然感到很悲哀，痛恨那些做發財大巴生意的人，簡直是送羊入虎口！我試圖告訴女孩玩百家樂會“久賭必輸”，但她不肯相信，說這次只是“運氣”不好，下個星期再去翻本。

我無語，太多失敗的人把“運氣”當做藉口。一把輸贏確實是運氣，10000把輸贏就是大數定理（勝率大者幾乎必勝）。在賭場中那些莊家穩操概率優勢的遊戲中反復下注，輸光豈非只是時間問題？所以有句話說：賭場不怕你贏，就怕你不來。

投資也是同樣的道理。股市比賭場好一些，長期看應該是正回報的遊戲。但是由於做莊、內幕交易、印花稅等因素，普通投資者如果“賭”的太頻繁，回報率很難跑贏大市，甚至可能“久賭必輸”。所以，別相信市面上那些教人“快速致富”的所謂“秘訣”，99%是浮雲，99%是忽悠。最重要的招數不是怎麼出招。

日本江戶時代有位“劍聖”宮本武藏，曾與人決鬥六十餘次，未嘗一敗。他除了技藝出眾，還有個秘訣：從不和比自己厲害的人過招。

這就是賭客和投資者都必需牢記的第一招：沒有把握，絕不出手。

賭 博與投資系列之三：賭場的優勢何在

上次說到，賭場不怕你贏，就怕你不來，因為賭場遊戲基本都是“久賭必輸”。很多玩家迷信“運氣”，而經營賭場的人相信概率，這就是輸家和贏家的差別。

例如輪盤賭（見下圖），博彩中玩家可以押任何一個數字，如果轉盤上的小球正好停在這個數字上，賭場賠35倍。聽著很誘人對吧？電影《卡薩布蘭卡》中那個從歐洲逃難出來的小青年接連押中幾手22，去美國的旅費就有了。實際情況如何呢？我們來簡單分析一下。

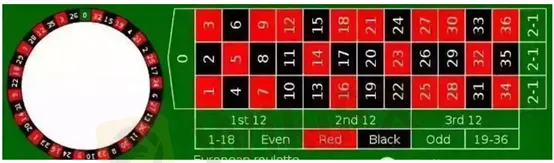
如果只有1-36這36個數字，那麼玩家每次押1元，平均每36把贏一次，贏的35元正好抵消另外35把輸的錢。但賭場在輪盤左邊加了個“0”，玩家的贏面變成了1/37，贏的35元不足以抵消另外36把輸的錢，賭場佔據了1/37=2.70%的概率優勢，也就是說玩家每押100元，平均要輸2.7元。這還是“仁慈”的歐洲式輪盤賭，美國人覺得還不夠黑，又加了個“00”（見下圖）。現在平均38把押中一次，玩家的劣勢擴大了到5.3%。

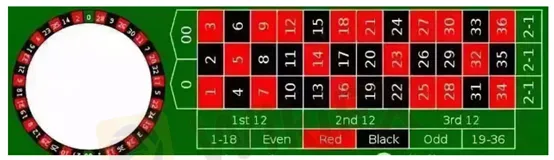
除了押單個數字，輪盤賭還有押紅黑等其他玩法。無論是1賠35的單個數位，還是1賠1的押紅黑，賭場的贏面都一樣。但兩者之間仍有個重要差別：押單個數字的輸贏波動顯然比押紅黑大的多。此處先簡單提一句：贏面和波動性是賭 博和投資中極為關鍵的兩點。“久賭必輸”的賭 博最好不要碰，實在要玩就挑輸贏波動性大的；“久賭必贏”的投資則應該選波動性小的。關於這個原理，後文將詳細討論。

回到賭 博，絕大部分賭場遊戲都設計的和輪盤賭類似：賭場擁有概率優勢。這些遊戲中，玩家如果只玩幾手還可能靠“運氣”贏點錢，長期玩下去幾乎必輸，數學中稱之為“大數定理”（LawofLargeNumbers）。

然而賭場機關算盡，還是被數學家找到了一處破綻。

賭 博與投資系列之四：21點的老故事

1960年代初，一位名叫索普（EdwardThorp）的美國數學家利用剛出現不久的電腦找到了21點遊戲中的機會，發展出一套通過計牌（cardcounting）打敗賭場的方法。索教授理論付諸實踐，用自己的計牌法連連大勝賭場，很快上了黑名單，眼看賭不成了，於是索某人就寫了一本書！

索普的《戰勝莊家》（BeattheDealer）狂銷70萬冊，榮登《紐約 時報》暢銷書榜（想起了我的《亂世華爾街》，慚愧中...），版稅收入遠遠超過了賭 博所得。這也再次說明一個道理：賣鏟子比挖金子容易賺錢。

索普計牌法的原理並不難。先講講21點的規則：玩家和莊家（賭場）對賭，看誰手中牌的點數之和更接近（但不能超過）21點。10，J，Q，K都算十點，2至9按各自點數計算，A可以算1點也可以算11點。例如下面的一手牌可以算8點，也可以算18點。

牌局開始，玩家和莊家各發兩張牌，莊家的牌一明一暗（例如下圖）。然後玩家先做決定：可以抓牌，做加倍等特殊行動，或在任何時候選擇“停”。如果玩家超過21點（爆牌）就直接輸了，否則“停”後輪到莊家行動。莊家不能“見機行事”，只能按固定規則：手中的牌達到17點或以上必須“停”，否則必須抓。最後雙方比誰的牌更接近21點。

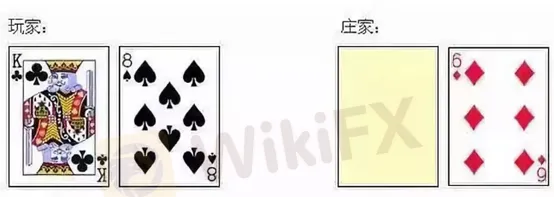
此外還有個特殊規定：一張A和一張十點牌（10，J，Q，K）叫“黑傑克”（Blackjack），拿到者直接取勝。如果玩家拿到黑傑克，可贏取1.5倍籌碼。莊家拿到黑傑克只能贏取1倍籌碼。

很明顯，21點遊戲中莊家和玩家各有優勢。莊家的優勢在“後發制人”：玩家如果先爆牌，莊家可以不戰而勝。而玩家的優勢在於靈活機動，可以根據自己的牌和莊家暴露的那張牌決定戰術。此外，黑傑克3：2的賠率也有利於玩家。

十點牌和A越多，出現黑傑克的機會越多，也越容易爆牌，玩家“機動靈活”的優勢更有價值。反之，3，4，5，6等小牌越多，爆牌的可能性越小，對莊家比較有利。索普時代的21點多用1副或2副撲克牌，當牌剛洗好時，賭場佔據0.5%左右的概率優勢。妙處在於，隨著牌局進行，某些時候大牌和A的比例會變高，概率會轉為對玩家有利。索普戰勝賭場的方法就是：通過計牌估算概率，當形勢有利時下大賭注！

一代宗師索普發明了計牌法，又寫了一本暢銷書，然後大徹大悟，上華爾街發財去了，後來又在對沖基金領域闖出了一片天地。索某達人也！

至於賭場這邊，從此出現了一批掌握了索氏武功的“計牌客”(cardcounters)。賭場方面想盡辦法將計牌客拒之門外，計牌客們則挖空心思突破封鎖。貓和老鼠的遊戲玩兒了幾十年，90年代前後，江湖上又出了一樁奇事。

（請放心，故事講到最後一定會回到投資上。）

賭 博與投資系列之五：MIT計牌團夥

話說索普之後，賭場多了個抓計牌客的麻煩事。時間一長，賭場方面逐漸積累了一個黑名單。如果名單上的人在21點牌桌上被認出來，通常會馬上被“禮送出境”：您上別處玩兒去吧！

八十年代某個時期計牌“案件”高發，賭場雇來的偵探把各處收集的黑名單放在一起研究，發現了一條重要線索：不少計牌客的住址都在麻薩諸塞州劍橋市附近！麻省劍橋您也許沒聽說過，但位於此地的兩所大學您不可能沒聽說過：哈佛、麻省理工（MIT）。難不成那幫研究相對論的智力超常同學們盯上了賭場？

後來真相逐漸浮出水面，果然有個以MIT學生為主的計牌團夥！這是個“商業化”運作的組織：有人出賭本，有人負責管理，有人上陣計牌，整個“投資”和“風險控制”模式頗有對沖基金的風範。團夥“作案”的最大好處是可以避免單個賭客面臨的風險：21點輸贏波動性很大，任你技術再高，短期內運氣不好也可能輸光賭本，集團作戰能分散這種風險。此外，MIT賭客們還使用了某些“多人戰術”。比如，邁克爾負責計牌，每把只押小注，當形勢有利時就拋出預先約好的暗號，此時扮作闊少的詹姆斯走過來，一把押1000美元。

MIT團夥前後運營了十幾年，MIT和哈佛等學校都有人參與，其中還有得過奧賽金牌的中國人。鐵打的營盤流水的兵，反正麻省劍橋一帶最不缺的就是數理天才。該團夥的盈利據說以百萬美元計，後來還有個作家專門把MIT團夥的事蹟添油加醬寫成了一本書，也上了《紐約 時報》暢銷書榜——又一個賣鏟子掙錢的。

到了九十年代中期，美國經濟一片榮景，團夥成員們紛紛前往矽谷、華爾街等處發展，MIT計牌團夥也就漸漸風流雲散了。這似乎也證明了一個道理：年輕人有正經事做，“犯罪率”就會降低。

又過了若干年，來自中國的漁陽同學偶然接觸到21點計牌這回事，大感興趣。我那時候土，沒聽說過索普，也不知道索宗師的書只賣十幾塊錢一本，花了100美元從一個叫卡多薩的大忽悠手裡買了本所謂“秘笈”。雖然被賣高價鏟子的宰了一刀，畢竟是有了鏟子，我也要去賭場挖金了！

但此時的江湖，已不是當年的那個江湖了。

賭 博與投資系列之六：關於賭注的困惑

學會了計牌方法後，我興致勃勃地前往拉斯維加斯小試牛刀。結果還真不錯，贏了厚厚的一疊百元大鈔，這21點還真是個金礦啊！我住在紐約，不可能總去拉斯維加斯挖金，好在紐約附近也有美國第二大賭城大西洋城，於是我就成了那兒的常客。賭了一段時間後，我漸漸發現大西洋城的“金砂”不好淘，我總體上只能小勝，而且輸贏的波動性很大。仔細研究了一番之後我才發現：這大西洋城跟拉斯維加斯可不一樣。

前面講過，計牌客主要是看大小牌在剩餘牌張中的比例，大牌比例高於正常時就下大賭注。顯然，在兩種情況下比例最容易變高，第一種是剩餘牌不多的時候，第二種是21點遊戲只使用1-2副牌時。索普時代的21點賭局正好具有這兩個特點：只用1-2副牌，而且發牌員（dealer）會將牌幾乎用光才洗牌，所以大牌比例時常變高，計牌客有很多機會在形勢有利時下大注。

賭場方面自然也有高人出謀劃策，明白對計牌最好的“軟防禦”就是設法控制大小牌比例的波動，於是賭場就使出了兩條毒計。第一是增加21點的用牌，從1-2副普遍改為6-8副。很明顯，牌一多，大小牌比例就不容易變。第二是提早洗牌，避開比例最容易波動的情況。

拉斯維加斯賭場多，競爭激烈，賭場為了攬客還保留了一些1-2副牌的21點遊戲，我贏錢主要就是在那些賭局中。而大西洋城地理位置得天獨厚，紐約、華盛頓、費城三個人口密集區的賭客都往那跑，賭場不愁沒生意，因此21點遊戲的規矩特別“黑”：基本都是8副牌，而且洗的很勤。大小牌比例變高的頻率低了，自然也就不容贏錢了。

原來我的江湖，已不再是索普當年的江湖。

雖然如此，但比例還是有變高的時候，我對賭場也還有贏面。前面講過“大數定律”：只要有贏面，理論上講一直玩下去最後還是我贏。但理論歸理論，實踐中有個重要制約：我的賭本有限，輸光了就不能玩兒了。大數定律只是說“革命最終會勝利”，可沒擔保你不會在“革命勝利前犧牲”。21點輸贏波動性那麼大，要是趕上一隻“黑天鵝”（BlackSwan,指微小概率事件）不就“光榮”了嗎？

假設我只有一萬美元賭本，好不容易等到我方對賭場佔據了1%的概率優勢，現在發牌員說：

“Placeyourbets.”（請下注。）

我押多少呢？20美元？平均才贏2毛錢，沒啥意思。押2000美元？趕上一隻不太黑的天鵝（連輸5把）我就輸光了。看來20美元太少，2000美元太多，最佳賭注應該在兩者之間。究竟應該押多少呢？

一位高人早就給出了答案。

（逐漸要講到投資理論了。）

賭 博與投資系列之七：凱利公式

上次說到，形勢有利時如何下注很需要技巧。押太少了浪費機會，押太多了“犧牲”的風險大增。什麼才是不多不少的合適賭注呢？1956年，科學家凱利（JohnKelly）就此發表了論文，提出了著名的凱利公式。

f*=(bp-q)/b

其中，f*=投注金額占總資金的比例

p=獲勝的概率

q=失敗的概率，q=1-p

b=賠率，例如在輪盤賭中押單個數位，b=35，押紅黑，b=1。

上篇中講到的21點下注問題，假設總賭本10,000美元，玩家取勝的概率是51%，賠率1：1（實際勝率和賠率略有偏差，但相距不大），那麼凱利公式給出的最佳賭注是：

$10000*(1*0.51-0.49)/1=$200

我知道很多人看到數學公式就頭大，但要玩好賭 博和投資沒法不用到數學。最重要的不在於帶公式計算數字，而是要弄明白公式背後真正的“意思”。

首先，公式中分子的bp-q代表“贏面”，數學中叫“期望值”(expectation)，凱利公式指出：正期望值的遊戲才可以下注，這是一切賭戲和投資最基本的道理，也就是前面講的“沒有把握，決不下注”。

其次，贏面還要除以“b”才是投注資金比例。也就是說贏面相同的情況下，賠率越小越可以多押注。這一點不容易直觀理解，我們用個例子來說明。下面三個正期望值的遊戲，你看看選哪個：

1.“小博大”：勝率20%，贏了1賠5，輸了全光。bp-q=5*20%-80%=20%

2.“中博中”：勝率60%，1賠1。bp-q=1*60%-40%=20%

3.“大博小”：勝率80%，1賠0.5。bp-q=0.5*80%-20%=20%

三個遊戲的數學期望值一樣，都是20%，或者說押100元平均贏20元。按大部分國人的賭性，恐怕會選“小博大”遊戲吧？但是用凱利公式中的“b”一除，“小博大”遊戲只能押總資金的4%，“中博中”可以押20%，“大博小”可以押40%。贏錢速度“大博小”快多了！前面不是講過“久賭必贏的遊戲應該選波動性小的”嗎？說的就是這個了。

現實中，愛玩“小博大”的多半是賭客。誰愛玩“大博小”呢？賭場！華爾街的職業投資家們很多玩的也是“大博小”，因為便於使用杠杆（押大賭注）。關於這點後面還要詳細講。

最後，凱利公式指明了風險控制的至關重要性：即便是正期望值的遊戲也不能押太大的賭注。從數學上講，押注資金比例超過了凱利值，長期的贏錢速度反而下降，還會大大增加出現災難性損失的可能性。舉個極端的例子，如果你每手都押上全部資金，那麼不管你贏過多少錢，只要輸一次就立刻破產。正所謂：辛辛苦苦幾十年，一夜回到解放前。

為什麼投資界賠到傾家蕩產的盡是一些局部技術不錯的老手呢？原因多半在“賭注太大”。上世紀初有位大宗師級別的投機客一世英名就毀在了這上面。

賭 博與投資系列之八：利弗莫爾敗走麥城

在凱利公式問世16年前的1940年11月28日，一位曾經威震華爾街的獨行俠在紐約沃爾道夫飯店的衣帽間裡拔出了手槍，他匆匆給妻子留下了一張便條：“...我已厭倦了戰鬥...這是唯一的解脫。”然後飲彈自盡。

傑西-利弗莫爾（JesseLivermore），不朽名著《股票作手回憶錄》的主人公，就這樣悲涼地結束了傳奇的一生。

如果你還沒看過《股票作手回憶錄》（ReminiscencesofaStockOperator），我強烈建議補上這一課。不少世界級的對沖基金經理都極為推崇此書。跟隨主人公的人生起伏，你可以領略百餘年前紛亂而又生機勃勃的美國金融市場的風貌，並驚詫於世間竟有利弗莫爾這般奇才。他身處“原始時代”，居然總結出了許多現代投資者奉為經典的規律：諸如賺錢時才可加碼，虧錢時應當止損，不要輕信他人觀點或所謂“內幕消息”，以及一套完整的“坐莊”手法。

更令人嘆服的是，利弗莫爾不但是理論家，而且是實踐家。他的交易人生幾起幾落，從白手起家到1907年時的數百萬美元身價，再到1929年時的1億美元身價！那時汽車才賣幾百美元一輛，利弗莫爾完全靠交易賺到的1億美元相當於今天的100億美元以上！

這樣一位不世出的奇才後來卻在市場上盡失巨額財富，最後演出了本文開始時那悲涼的一幕。利弗莫爾是怎麼走的麥城呢？文獻並無具體記載，但如果仔細分析他的交易習慣，就不難發現蛛絲馬跡。

利弗莫爾的交易生涯始於BucketShop（可意譯為“股票賭場”）。19世紀末，美國股票市場十分活躍，而技術進步使遠離紐約的普通人也有機會“即時”參與股票投機：與電報線相連的自動報價機可以隨時將紐約交易所的最新成交價傳遍全國。當時很多人想參與投機，但缺乏買賣股票的資金，奸商們借機將這批人吸引到“股票賭場”。

賭場中有自動報價機，玩家們似乎在交易股票，實際上是在賭大小。舉個例子，某股票的最新報價是80美元，玩家只需交納1美元保證金就可以買“大”，如果報價機上出現了79美元或更低的價格，那麼對不起您輸光了；如果報價機上打出了81美元，玩家可以兌現1美元盈利，也可以繼續等。

股票賭場的奸商們怎麼賺錢呢？除了利用群眾們經常押錯的特點外，他們還串通某些券商操縱市場。比如在80美元的價位上很多玩家押了“大”，賭場莊家就指使紐約交易所的同夥打壓股價，只要自動報價機上打出一個79美元的價格，賭場就通吃了押大的籌碼。

當時還很年輕的利弗莫爾沒什麼錢，在股票賭場裡混，逐漸練就了根據報價預測市場價格(ReadTape)的本領。那時候沒有電腦，更沒有即時K線圖，利弗莫爾的“讀盤”功夫實際就是技術分析的原型。但我很懷疑他也在股票賭場裡養成了“壞毛病”：押注太大。

從凱利公式的角度分析，股票賭場的超低保證金其實是賭徒們的“殺手”。杠杆那麼大，押注遠超凱利最優值，輸光是遲早的事。那時的美國正規金融市場的交易保證金也很低。利弗莫爾後來的交易經歷表明，他一直保持了超大賭注的風格。讀他的交易歷程簡直令人心驚肉跳，股票、棉花、大豆，不管什麼都是超高杠杆全倉操作，這固然成就了利弗莫爾的傳奇偉業，也令他數次破產。

所幸幾次都有貴人相助，利弗莫爾才得以抓住1907年，1915年和1929年幾次重要機會屢攀高峰。但智者千慮、終有一失，我很懷疑正是“押注太大”的毛病令利弗莫爾在身價達到1億美元的短短數年後就輸光了所有錢。最後一次，他沒能東山再起。

如果利弗莫爾將基於凱利公式的資金管理方法和他高超的市場把握能力結合在一起，這位天才會創造出怎樣的奇跡呢？

歷史沒有如果。利弗莫爾已如流星劃過，也許他早生了幾十年。資金管理和風險控制的理論在50年代才開始成型。凱利公式指出：贏面大、波動性小的遊戲可以押較大賭注。那麼如何量化“贏面大，波動性小”呢？與凱利同時代的一位學者提出了一個著名的指標。

賭 博與投資系列之九：夏普比率

上次談到，評估投資機會的優劣應該從收益期望和風險兩方面綜合考慮。如何量化這一思想呢？1950年代，有人提出用回報期望和波動性的比例作為衡量投資機會的指標。1966年，學者夏普（WilliamSharpe）在此基礎上提出了著名的夏普比率（SharpeRatio）：

S=(R–r)/σ，其中：

R=投資的回報期望值（平均回報率）

r=無風險投資的回報率（可理解為投資國債的回報率）

σ=回報率的標準方差（衡量波動性的最常用統計指標）

夏普比率S越高，投資機會的“品質”越高。舉個例子：

甲投資：超額（超出國債）回報期望10%，標準差20%，夏普比率為0.5

乙投資：超額回報期望5%，標準差5%，夏普比率為1

乍一看，甲投資回報期望高，似乎是比較好的機會。其實乙投資更勝一籌（通常情況下），因為它的夏普比率高，意味著投資者用1個單位的“風險”能換取更多的回報期望。從杠杆投資的角度也可以得出同樣的結論：假設投資者以r貸款利率融資，在乙投資機會上加1倍杠杆，那麼“杠杆化”的乙投資就變成了10%回報期望，10%標準差，與甲投資的回報期望相同，而風險較小。

夏普比率多高才算“好”呢？我們來看一個實際的例子：美國股市的長期年平均回報率約為10%，波動性約為16%，無風險利率約為3.5%，因此夏普比率約為0.4（來源：維琪百科）。翻譯成白話就是：投資美股指數的年均回報率約比無風險利率高6.5%，但平均6年中有1年的回報率低於-6%（1倍標差之外）。

對於長線投資的散戶而言，投資美股的風險/回報還算說的過去。如果是對沖基金經理，這樣的夏普比率就太低了：假設你的目標是20%年回報率，就必需用2.5倍杠杆（回報期望=2.5*10%-1.5*3.5%≈20%），也就意味著平均6年中有1年的回報率將低於2.5*（10%-16%）-1.5*3.5%=-20%。你賠了超過20%，客戶大概就要跑光了。

一般說來，夏普比率超過1才是“好遊戲”。這種機會在“簡單投資”中並不多見，因此職業投資者常常利用對沖手段“改造”投資遊戲，提高夏普比率。

《亂世華爾街》中多次提到，對沖與杠杆是一對孿生姐妹，兩者往往配合使用，說得就是這個原理。

例如，你發明了一種方法，用各種資產相互對沖得到夏普比率為2的投資機會，那你就可以大膽加杠杆（數學好的同學們可以自己計算賠錢的概率），投資者大概要追著給你的對沖基金投錢了。

但對沖+杠杆的投資方法通常有個“練門”：需要借很多錢，對流動性要求高，因此遇到突發性危機往往會出問題，《亂世華爾街》中就分析過LTCM和高盛GlobalAlpha基金的例子。

夏普比率也存在缺陷，它假設回報是正態分佈，而實際的投資回報分佈有“肥尾”（賠大錢的概率高於正態分佈的估計），因此單純根據夏普比率挑選投資機會存在問題，也容易被“操縱”。這個話題此處暫不展開討論。

對普通投資者而言，夏普比率提示要從風險和回報的角度綜合考慮，挑選“性價比”高的投資。這正是前面的文章中提到的觀點：正回報的遊戲要挑波動性小的，負回報的遊戲如果非得玩，就挑波動性大的。

總之，夏普比率越高越好。

夏普比率講的是如何挑選“遊戲”，而凱利公式講的是選好了遊戲後如何下注才能取得最優的長期回報率。現在我們就把兩種方法配合起來使用，看看21點計牌到底是不是條發財的路。

賭 博與投資系列之十：關於夏普比例的補充說明

夏普比率的幾個問題，主要集中在幾個方面：

第一個問題：關於美國股市的那個例子中，“平均6年中有1年的回報率低於-6%”是怎麼算出來的？

夏普比率假設投資回報符合正態分佈（見下圖）。從數學上說，大量獨 立隨機事件之和一般符合正態分佈。例如不停地扔硬幣，正面為1，反面為-1，大量重複後結果之和就符合正態分佈。前面的博客提到過，學術界流行“有效市場理論”：股市每一步運 動方向都是獨 立隨機的，相當於不斷“扔硬幣”，最後回報率當然就符合正態分佈。再講下去就是數量金融的基礎課《隨機過程》了，就此打住。

正態分佈的假設雖不完美，但不失為理解問題的基本框架。下圖顯示了正態分佈的概率數值。例如，回報率在0倍到0.5倍標準差之間的概率為19.1%（圖中綠色部分）。同理，回報率低於-1倍標準差（圖中橙色部分）的概率約為16%。應用於美國股市（回報率中值10%，標準差16%），年回報率低於-1倍標準差，即10%-16%=-6%的可能性約為1/6。“平均6年中有1年的回報率低於-6%”就是這麼估算出來的。

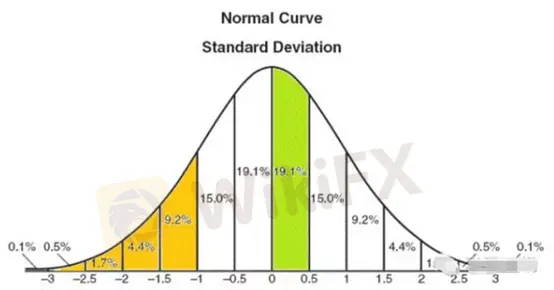
第二個問題：夏普比率的假設有沒有不符合實際之處？

當然有。正態分佈的假設就不完美。實際上，股市運 動不完全“獨 立隨機”，否則我們就不需要費心研究什麼規律了。例如在金融危機中，股市運 動有很強的序列相關性（serialcorrelation），即所謂“趨勢”，導致實際的股市回報有“肥尾”現象，就是說“跑到極端位置”的可能性高於正態分佈的估計。另外，夏普比率中的“無風險回報率”r是個模糊的概念，投資者的融資成本也不是r。再有，波動性的測算也並非簡單問題。其他不一一介紹了，已有N多學術論文討論夏普比率的局限性及改進方案。

第三個問題：夏普比率對普通投資者到底有什麼用處？

主要是思維上的啟示：投資不能只看回報率，還要看擔多少風險。下次再有人告訴您“我過去三年平均回報30%！”的時候，您可以“弱弱”地問一句：“波動性多大？”。下篇博客中，我們來看一個對沖基金的真實例子。

賭 博與投資系列之十：對沖基金業績的分析實例

評估投資績效不能只看回報率，還要考慮風險因素。現在我們就來看一個對沖基金的實際例子。下表是幾個知名大型對沖基金的平均年回報率（資料來源：滙豐銀行研究報告）。這些基金管理資產均在10億美元以上，開業時間均在5年以上。您會把錢投給哪家基金呢？

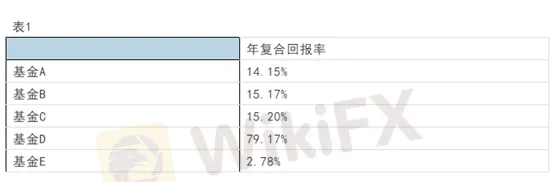
您會選年回報率79%的基金D，對嗎？恭喜，您選中的正是在金融危機中大舉做空次貸類產品，豪取幾十億美元利潤，出盡風頭的PaulsonCreditOpportunitiesFund。創建並管理該基金的保爾森（和前任美國財長保爾森同姓，但沒有親屬關係）也一舉成為最著名的基金經理之一。

但我們剛剛討論過：不能只看回報率，還要考慮風險。表2中列出了各基金的波動性和夏普比率估值（假設無風險回報率為3%），您看過之後有何想法？

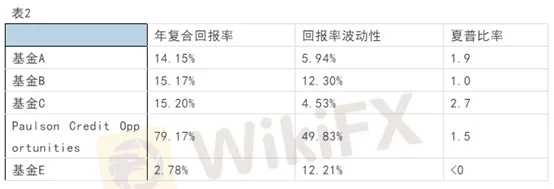
從波動性和夏普比率的角度一分析，情況有點複雜了。基金C回報率雖然只有15%，但波動性不到5%，因此夏普比率高達2.7，竟比保爾森基金的1.5高出近一倍！換言之，基金C的波動性只有保爾森基金波動性的十分之一，假設投資者只願意承擔固定的波動性風險，那麼他可以投資1元在保爾森基金或10元在基金C，風險都差不多，而投資基金C的總回報更高！

基金C是MillenniumIntlLtd（千禧年基金），對沖基金業界的常青樹，旗下經理中曾有若干華裔高手。站在投資者角度，到底是選“賺得狠”的保爾森基金，還是選“賺得穩”的千禧年基金，還真有點難以取捨。另外，基金A和基金B的夏普比率都明顯高於美國股市的0.4，也是不錯的投資選項。而基金E的回報率竟低於無風險利率，“境界”太低了。

再進一步分析，僅用夏普比率做比較，好像對保爾森基金“不太公平”：它的波動性雖然高，但主要是“向上波動”，在盈利嗖嗖漲的過程中產生的“波動性”，其實並非風險。投資者怕的是賠錢，尤其是一下賠掉百分之幾十。所以衡量風險還應該考慮“最大跌幅”，即各基金歷史上從最高點“回落”的最大比例，見表3。

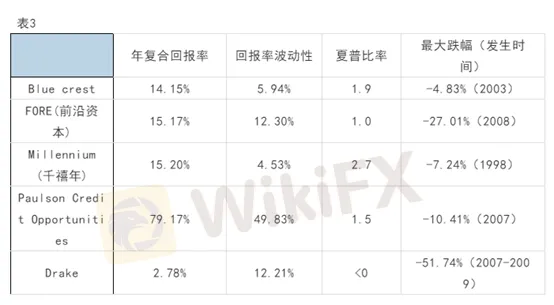
現在更有意思了，基金A（BluecrestCapital）的最大跌幅只有不到5%，而且發生在2003年。該基金在2007-2008年的大危機中竟然避免了重大損失，相當有吸引力。Bluecrest和千禧年都屬於“賺得穩”類型，都躲掉了次貸危機，兩者似乎難分伯仲。它們和保爾森基金相比，可謂春蘭秋菊、各擅勝場，因此三支基金都是機構投資者青睞的對象，管理資金分別達到86億美元，100億美元和63億美元。看來人家能“做大”是有道理的。（注：不少“名牌”基金為保持回報率，已不再接收新投資。）

基金E（DrakeAbsoluteReturnFund）也曾是管理數十億美元的大型基金，但它在金融危機中遭到了50%以上的巨大損失，令投資者失去信心，紛紛撤資，所以Drake現今管理的資本已只有2億美元。可見，不管做的多大，如果不注意風險也可能“一夜回到解放前”。前文中講了利弗莫爾，此處的Drake也是活生生的例子。

最後來看看基金B，它的長期年複合回報率15%，夏普比率1，綜合指標不錯，雖然在2008年一度遭到27%的損失，但已成功渡過危機。可以說基金B具有相當實力，因此它也成為管理10幾億美元的大基金。該基金的名字是FORECapital（前沿資本），瓢把子MatthewLi（黎彥修）是華人在對沖基金界的一面旗幟。讓我們為華裔高手的成功鼓掌！

從這個評估投資業績的真實例子，我們可以看到夏普比率和最大跌幅等風險指標的用處。初學投資者常有只重回報、不看風險的毛病。凱利公式也好、夏普比率也好，其實都告訴我們一件事：要在回報和風險之間尋找平衡。